【ベストコレクション】 等差数列の和 公式 シグマ 895550-等差数列の和 公式 シグマ

 等差数列の和の公式 等差数列の和 S n = ∑ i = 1 n a i は以下のように書き換えられる。 (2) S n = 1 2 n ( a 1 a n) これが等差数列の和の公式だ。 ガウス君の問題だと、 n = 100, a 1 = 1, a 100 = 100 なので、 S 100 = 1 2 100 × ( 1 100) = 5050 というように、公式 (2)を使えば（位相が等差数列なら）複素指数関数と等比数列の和の公式を用いて三角関数の和を計算することができる： ∑ k = 0 n sin ⁡ ( θ k ϕ ) = sin ⁡ ( ( n 1 ) ϕ 2 ) sin ⁡ ( θ n ϕ 2 ) sin ⁡ ϕ 2 \displaystyle\sum_{k=0}^n\sin(\thetak\phi)=\dfrac{\sin(\frac{(n1)\phi}{2})\sin(\theta\frac{n\phi}{2})}{\sin\frac{\phi}{2}} k = 0 ∑ n sin ( θ k ϕ ) = sin 2 ϕ sin ( 2 ( n 1 ) ϕ ) sin ( θ 2 n ϕ )一般に，初項 a，公差 d，項数 n の等差数列の末項を としますと，初項から第 n 項までの和 Sn は， Sn=a (ad) (a2d) (d) (3) となります。 また，S10は上の例と同様に， Sn= (d) (2d) (ad)a (4) と書けますので， (3)と (4)の辺々加えますと， となります。

数列の基本５ 階差数列の考え方は簡単 階差数列の公式

等差数列の和 公式 シグマ

等差数列の和 公式 シグマ-等比数列の和にはシグマの計算公式が使えない シグマ（Σ）は和を表す記号で、公式では無いということは何度も言ってきたのでわかっていると思いますが、 計算公式も3つだけはあるというのも知っていますよね。 \displaystyle \sum_ {k=1}^n k=\frac {1} {2}n (n1) \displaystyle \sum_ {k=1}^n k^2=\frac {1} {6}n (n1) (2n1) \displaystyle \sum_ {k=1}^n k^3=\left\ {\frac {1} {2}n陈金跃 等差数列求和公式的变换与意义j 中学数学研究, 02(12)4142 3 刘锡凤 等差数列求和公式的应用教学设计j 中国科教创新导刊, 13(2)9495 4 齐龙新, 王红艳 等差数列求和公式变式的灵活应用j 高中数理化, 09(2) 5 杜莹梅 等差数列求和公式的

等差数列と等比数列の共通項 大学受験の王道

等比数列の和の公式② 公比が1の場合の等比数列の和を求めましょう。 r = 1 の場合は同じ数字が並び続ける数列です。 この数列の和は（初項）×（項数）で求めることができます。 したがって、 r=1 のときはこの公式を使いましょう。 \displaystyle S_ {n}=na こんにちは。 da Vinch (@mathsouko_vinch)です。 等比数列の和の公式今回はまず前回とは違った形の和の公式を考えていきます。次の和はどうなるでしょう。 $$\sum_{k=1}^n 和の中抜けとは？ 分数や連続整数の積の総和を求める方法を例題付きで紹介！ 1 和の中抜けとは 12 数列の総和の公式が使えないときに和の中抜けは有効 2 和の中抜けが有効な例3

数学B（数列）：シグマの公式 数学B 対象 高校生 再生時間 849 説明文・要約 ※ 1つ目の公式の説明は、「シグマの意味」の動画で使用しているものと同一です。 以下の3つの公式を覚えてください！ 〔コツ〕 ・「1乗」は、 連続する2つの階差数列の項番号は，元の数列の 小さい方の番号 と同じです。 b n = a n1 a n b n →a n 例 次の数列において， 6＋5＝11 6＋5＋7＝18 6＋5＋7＋9＝27 6＋5＋7＋9＋11＝38 です。 ※ 高校では，Σの部分は「実際に和を表わしていること」が条件になります。等差数列のn項の値と初項からn項までの総和を計算します。 S n = a ( a d ) ( a 2 d ) ⋯ ( a ( n − 1 ) d ) S n = a ( a d ) ( a 2 d ) ⋯ ( a ( n − 1 ) d )

式の左辺は、第1項から第n項までの等差数列の和を表していますね。一方、 第n項までの等差数列の和 は、公式より 2(a 1 a n)/n でしたね。これがポイントにおける右辺の式になっています。数列11 シグマ3 累乗のあるシグマの計算 高2数学 数b Youtube 数学b 和の記号シグマと累乗の和の求め方とコツ 教科書より詳しい高校数学 総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ Sシグマの公式まとめと前回 https//googl/dr6wRD 次回 https//googl/OWfUAc動画のプリント（19ch） http//www19chtv/サブチャンネル とある男が

数列の基本５ 階差数列の考え方は簡単 階差数列の公式

48s96ub7b0z5f Net Tousakakerutouhi

等差数列とその和 ・等差数列の隣接する項の関係を考 察し、その一般項や第n項までの和 を求めることができる。 ・一般項を表すことができたか。 ・等差数列の和の公式を理解し、そ れを適切に利用で 等差数列の和の公式から使っていきます。 解説と照らし合わせてみてください。 内側から順に、 等差数列の和の公式 →シグマの分配法則 →2乗和と1乗和 →mについて整理 →mについての3次式とシグマの分配法則 →3乗和、2乗和、1乗和の公式A a r a r 2 ⋯ aarar^2\cdots a ar ar2 ⋯ と表せます。 これをシグマを使って表すと， a a r a r 2 ⋯ = ∑ k = 0 ∞ a r k aarar^2\cdots=\displaystyle\sum_ {k=0}^ {\infty}ar^k a ar ar2 ⋯ = k=0∑∞

数列の和の一問一答カード 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

数列公式集 Flashcards Quizlet

ポイント (等差)× (等比)の和， (2次式)× (等比)の和の解き方 和を書き並べて， 和から和に公比をかけたものを右にずらして引く． 公比をかけて右にずらして引くという操作は， 等比数列の和の公式 を導くときにもしたことですね． 下の例題と練習問題 はじめに、等差数列と等比数列の和の公式を確認しておきます。 等差数列の和の公式 等差数列の和は、Sn={(a1an)×n}/2、つまり $$S_{n}=\frac {\{(初項)(末項)\} \times (項数) }{2}$$ で 1．等差数列の和 初項$a$、公差$d$、末項$l$、項数$n$であるような等差数列の和$S_n$ $$S_n=\dfrac{1}{2}n(al)=\dfrac{1}{2}\{2a(n1)d\}$$ 2．等比数列の和 $$S_n=\begin{cases} \ \dfrac{a(1r^n)}{1r}=\dfrac{a(r^n1)}{r1} &(r\neq 1)\\ \ na &(r=1) \end{cases}$$ 3．数列の和の公式

3

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列は同じ数を何回も足していく（引いていく）という規則があるような数列ですから、出発点と足していく数がわかればいいのです！ 23シグマ（数列の和） 等差数列の和の公式は「1から100まで足す」計算と同じことをしていると覚えておこう 等差数列のときと似たような導入でかきます。覚えなくていい「等差数列の和」 算数は得意なのに数学が苦手なひとのためのブログまず、等比数列の公式として、 こんな感じで教わってるかな？ それとも みたいな感じ？ こんな感じで覚えてると、は？等比数列の和の公式について質問させてください。 先生のページでは、項比rから－1するという形になっていますが、 別の書籍等では、1から項比rをマイナスするという形になっているものもあります。 この違いは何に起因するのでしょうか？

3

等比数列の和がシグマで表記されている問題の解き方 月刊木村 清須市で営む塾での日々

Try IT（トライイット）のΣ と等差・等比数列の和の練習の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。のように、kの関数として表されるものを指す。31のような形式で表された数列 を等差数列、32 のような形式で表された数列を等比数列と呼ぶ。 数列の和は、以下の公式を使って求めることができる。 ∑n k=1 k = 1 2 n(n1) (33) ∑n k=1 k2 = 1 6 n(n1)(2n1) (34) ∑n k

数列 Sシグマの公式を使った計算をマスターしよう 数スタ

和の記号s シグマ の公式と 証明方法 高校生向け受験応援メディア 受験のミカタ

高校数学 B 数列 S シグマ のタイプ別頻出問題3選 応用問題に挑戦 やはり俺の考察ブログはまちがっている アニメ 数学

S計算 部分分数分解編 おいしい数学

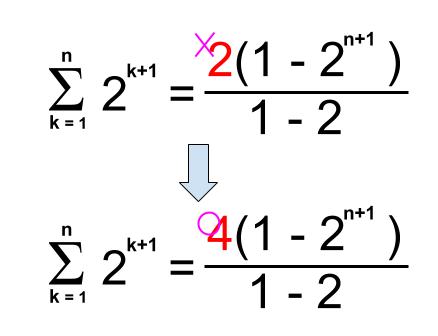
等比数列の和 計算の仕方

和の記号s シグマ の公式と 証明方法 高校生向け受験応援メディア 受験のミカタ

シグマ S とは 記号の意味や和の公式 証明や計算問題 受験辞典

無限 等 比 級数 の 和 等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Documents Openideo Com

高校数学b 階差を利用する和 根号型 対数型 階乗型 受験の月

このように初項と公差と末項が分かっている時にはどうやって解いたらいいのですか Clear

数列 奇数の和 を求める 大人が学び直す数学

等差 等比 の和 2次式 等比 の和 おいしい数学

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

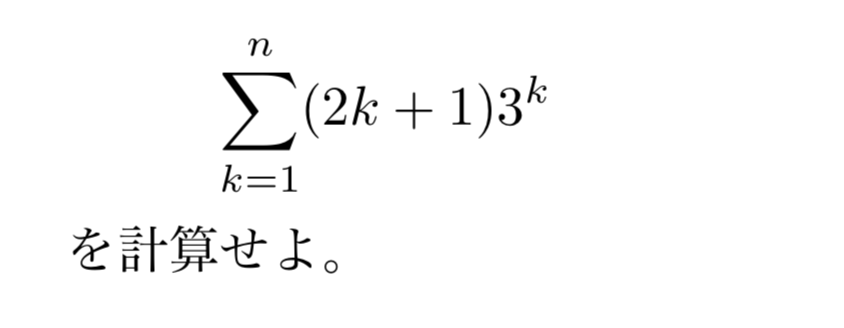
和の中抜けとは 分数や連続整数の積の総和を求める方法を例題付きで紹介 東大医学部生の相談室

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

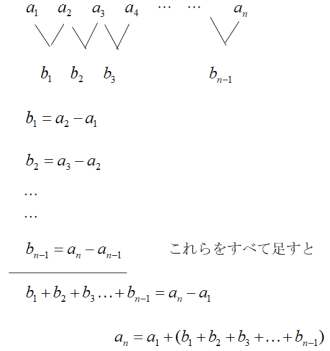
階差数列の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

高校数学b Sの性質と数列の和の公式 S公式 Sk Sk Sk 受験の月

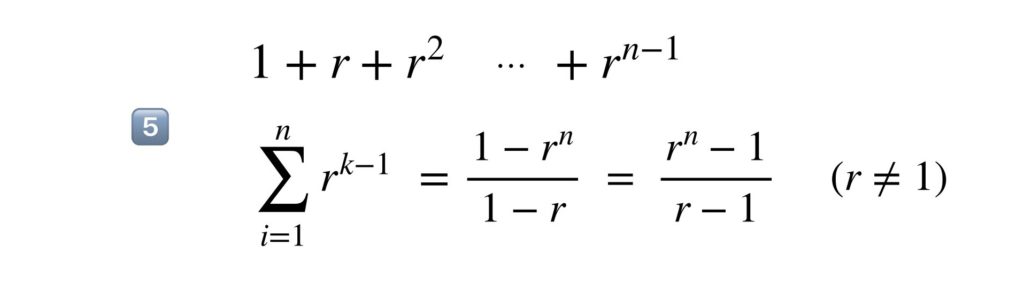
シグマの計算 苦手になるポイントを徹底解説 家庭教師の想い

数学b 数列 和から一般項を求める オンライン無料塾 ターンナップ

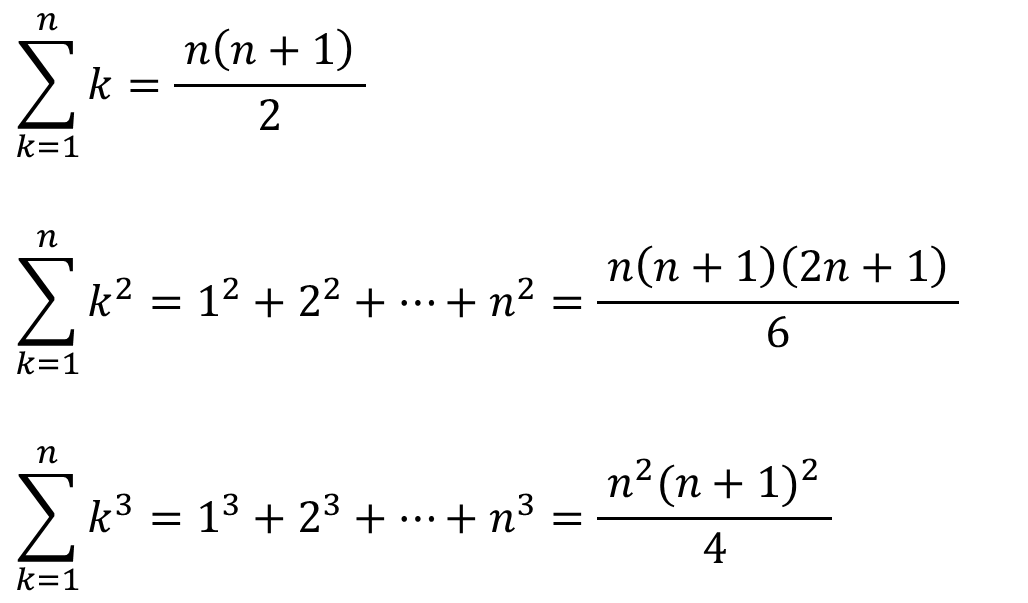
数学b 数列 シグマの公式 オンライン無料塾 ターンナップ

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

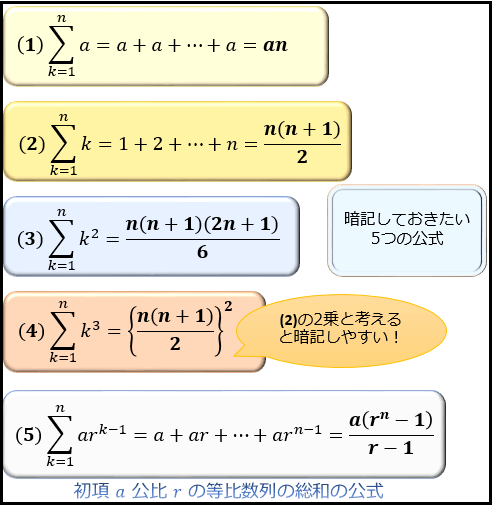
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

数列の和とs記号 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

階差型の数列 おいしい数学

1乗和 2乗和 3乗和の公式 導出法から理解しよう

数列 Sシグマの公式を使った計算をマスターしよう 数スタ

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

高校数学b 階差数列から一般項を求める １ 練習編 映像授業のtry It トライイット

48s96ub7b0z5f Net Tousa Suuretsu

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

等差数列と等比数列の共通項 大学受験の王道

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

群数列とは わかりやすいポイントと解法 例題と解答 解説つき 高校生向け受験応援メディア 受験のミカタ

数列の教え方 キムチャート 塾で高校生に数学を教える方法

1 の問題が 解説を見ても意味がよくわかりません Tt シグマの計算は分かるのです Clear

高校数学b S と等差 等比数列の和 練習編 映像授業のtry It トライイット

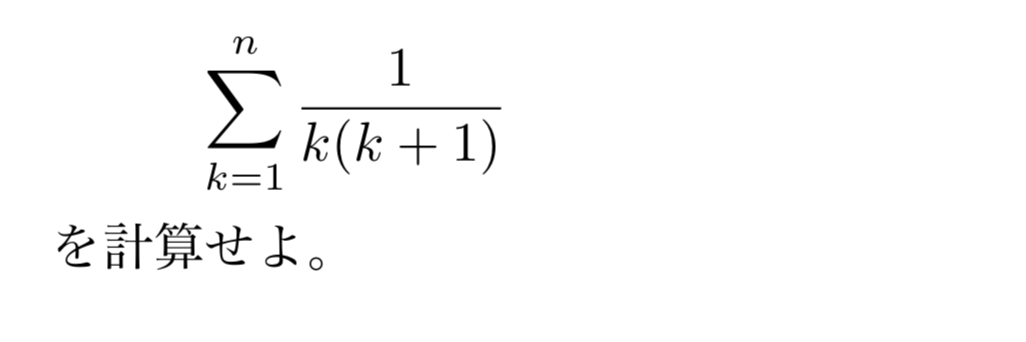
和の中抜けとは 分数や連続整数の積の総和を求める方法を例題付きで紹介 東大医学部生の相談室

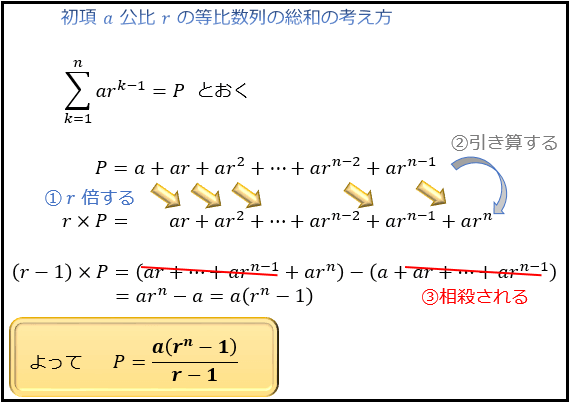
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

等比数列の一般項と和 おいしい数学

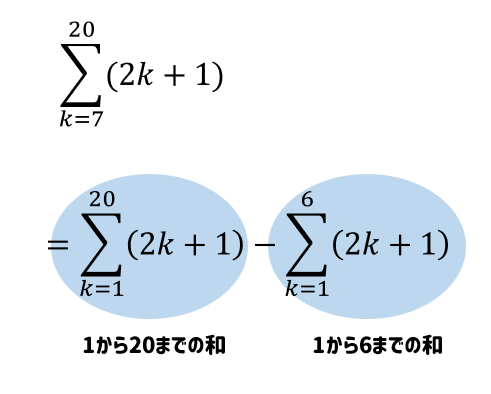
数列 Sシグマの公式を使った計算をマスターしよう 数スタ

シグマの計算 苦手になるポイントを徹底解説 家庭教師の想い

高校数学b 調和数列 逆数が等差数列 の一般項 受験の月

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

等差 等比型

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等差 等比 の和 2次式 等比 の和 おいしい数学

数列 公式は意味の分かる形で覚えよう 受験生応援し隊 Presented By Forest

階差数列

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

力をつけよう２ S 等差数列 等比数列 力をつけていいんじゃない

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

分数の数列の和 高校数学ｂ Youtube

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

階差数列

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

高校数学b 絶対値付き数列の和 S A K 受験の月

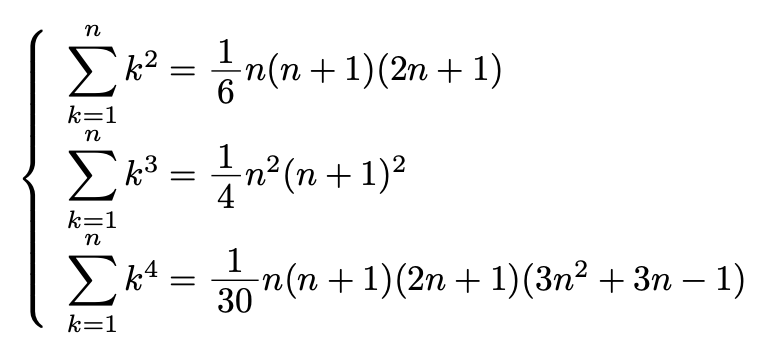
シグマの公式 2乗 3乗 4乗 の証明は 数列の和はこれでマスター 東大医学部生の相談室

高2 数b 等差 等比数列 公式まとめ 高校生 数学のノート Clear

等差数列の和 ｓₙ ａ ａₙ ｎ ワンセンテンス算数 Note

等差 等比型

シグマ記号sの考え方 数列の和を表すsの定義と性質

高校数学ｂ S公式 問題一覧 公式 覚え方 計算方法 学校よりわかりやすいサイト

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

等差数列や等比数列とシグマ計算s 大学受験対策にも タロウ岩井の数学と英語 Note

階差数列

1

高校数学b S と等差 等比数列の和 練習編 映像授業のtry It トライイット

48s96ub7b0z5f Net Shigumanokeisan

等比数列の和

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

高校数学b 等差 等比 型 2次式 等比 型の数列の和 受験の月

数b 数列について 9 1 2 2 4 2 4 6 2 4 6 8 この数列k項 数 高校 教えて Goo

等差数列 演習1 例題1 和の条件から初項と公差を求める 例題2 和の最大値を求める Youtube

S3のk乗はどうやって解けば良いのでしょうか ご回答お願いします Yahoo 知恵袋

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

和を求める時 左の問題はなぜ Sを使うのですか Clear

数学用語解説

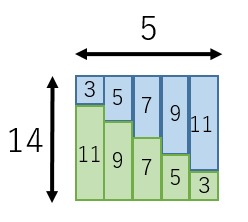
等差数列の和を計算する2つの公式 具体例で学ぶ数学

Q Tbn And9gcsksuzfvrfdxyebs50ns6jdnnyuhzxk9z645owq3zjlok2ztfva Usqp Cau

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

数学の質問です 写真のsの数列の和の公式が とても複雑でやや Yahoo 知恵袋

等差数列と等比数列の積の和の問題の解法ポイント 数列

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

例題で学ぶ高校数学 階差数列

数列と級数 京極一樹の数学塾

数列 Twitter Search

和を求める時 左の問題はなぜ Sを使うのですか Clear

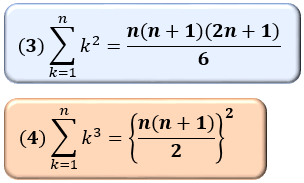
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

和の記号s シグマ の公式と 証明方法 高校生向け受験応援メディア 受験のミカタ

高校数学 B 数列 S シグマ のタイプ別頻出問題3選 応用問題に挑戦 やはり俺の考察ブログはまちがっている アニメ 数学

S計算 基本編 おいしい数学

Incoming Term: 等差数列の和 公式 シグマ,